7. Мягкие измерения и вычисления в интеллектуальных системах 

Концептуальные основы создания интеллектуальных систем (ИС) базируются на фундаментальных принципах, определяющих архитектуру системы и уровни ее управления. Теоретическая база  создания ИС формируется на основе эффективного сочетания накопленной системы знаний с новыми подходами и парадигмами искусственного интеллекта (ИИ). Среди них важная роль принадлежит методам и моделям, обеспечивающим формализацию и интеграцию знаний, механизм логического вывода, поиск решений и выдачу практических рекомендаций. Наряду с традиционными математическими методами здесь широко применяются достижения ИИ и новые принципы функционирования ИС, обеспечивающие наиболее сложные уровни ее иерархической структуры - самоорганизацию и самообучение. Использование этих принципов позволяет ИС <понимать> сложные процессы взаимодействия динамического объекта с внешней средой, <моделировать> свои действия о <обучаться> на своем опыте.

7.1. Концепция мягких вычислений

       Повышение степени интеллектуальности систем обработки информации в современных условиях достигается за счет использования математического обеспечения подходов и методов бурно развивающего в рамках теории ИИ нового научного направления, получившего название мягкие вычисления (soft computing) [35]. Фундаментальной основой этого направления являются теоретические принципы формализации знаний, используемых при организации проектирования и функционирования систем, с учетом их неточности и неопределенности, а также их алгоритмическая обработка при принятии решений или выборе операций поддержки целенаправленных действий [1], [2], [22], [35]. Принципиальными компонентами мягких вычислений являются нечеткая логика, теория искусственных нейронных сетей (ИНС) и генетические алгоритмы (ГА). При описании информационных и процедурных элементов мягких вычислительных процессов положения нечеткой логики позволяют формализовать неточность и неопределенность, а ИНС и ГА - организовать обучение в процессе выполнения вычислений и их высокопроизводительную реализацию.

       Рассмотрим динамическую систему, поведение которой в нечеткой среде описывается вектором состояния X={x_i} (i=1,:,n). На систему воздействуют внешние возмущения, характеризуемые вектором W={w_k} (k=1,:,K). Выходные координаты системы Y={y_j} (j=1,:,m) представляют собой регулируемые величины, зависящие от управляющих воздействий U={u_q} (q=1,:,Q).

       Общая схема функционирование ИС, осуществляющей оперативный контроль  и выдачу практических рекомендаций по управлению динамическим объектом, представлена на рис.3.9 . Исходная информация поступает от датчиков измерительной системы. Наблюдения фиксируются в дискретные моменты времени и характеризуют траектории измерений, образующих информационный вектор. Анализ имеющейся информации позволяет установить фактическое состояние динамического объекта и параметры внешних возмущений.

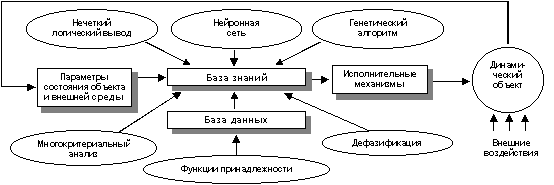
Рис.3.9.Поток информации при реализации концепции мягких вычислений в интеллектуальной системе

       Алгоритмы преобразования информации при реализации механизма логического вы вода в ИС обычно представлены на основе продукционных моделей [1] , [24] :

"If X, then Y, else Z" ;  (3.28)

(X RY (Z)).

      При интерпретации ядра продукции (3.28) в антецеденте импликации используются различные встроенные процедуры, основанные на применении аппарата статистического анализа, методов математического моделирования, методов качественного исследования дифференциальных уравнений на фазовой плоскости и др. Наряду с методами традиционной математики здесь находят также применение теория ИНС и ГА.

      Формализация нечеткого логического вывода в соответствии с конструкцией (3.28) осуществляется путем использования нечетких условных высказываний. Результат выполнения нечеткого условного оператора (3.28) характеризуется выражением

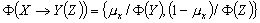
где X Y Z  - нечеткие множества, определенные на универсальных множествах U, V, W (XÎU, YÎV, ZÎW); m_x - функция принадлежности, характеризующая степень истинности   условия Х.

       Среди многих задач  обработки информации при функционировании ИС, решаемых в рамках концепции мягких вычислений, следует выделить задачу многокритериальной оптимизации. При реализации концепции мягких вычислений в этой задаче   элементы нечеткой логики позволяет обеспечить толерантность результата по отношению к неточности и неопределенности обрабатываемых информационных массивов, возможность ГА - находить субоптимальные решения, а ИНС - проверять ограниченное число найденных решений с целью определения оптимального из них. В результате удается избежать излишних вычислительных затрат (<комбинаторного взрыва>) с ростом размерности задачи [22], [34].

       Генетические алгоритмы - нетрадиционные оптимизационные структуры, в основу которых заложены некоторые особенности биологической эволюции на уровне механизмов  кодирования и наследования. Применение этого необычного математического аппарата открывает возможности использования новых подхода к решению задач классификации с использованием параллельных архитектур. Наиболее часто ГА находят применение в задачах оптимизации и представляют собой класс методов, обладающих наилучшими нелокальными свойствами.

      Формальное описание ГА дает зависимость [27]:

GA = (P_o, L, I, S, R, F, t),     (3.29)

P_o = (p₁,:,p_L); p_L - решение задачи, представленное в виде хромосомы; L - целое число (размер популяции); I - целое число (длина каждой хромосомы в популяции); R - отображение, определяющее рекомбинацию (кроссовер (crossover), мутация); F - функция оптимальности; t - критерий остановки.

       При использовании ГА в задачах оптимизации простой рандомизированный перебор при поиске минимума по методу Монте-Карло можно заменить на хранение популяции лучших с точки зрения функционала объектов и добавления новых объектов посредством мутации одного объекта, либо посредством кроссовера - обмена подобными частями у двух случайных объектов. Мутация - это почти полный аналог случайного шага в методе Монте-Карло, а кроссовер и популяция привлечены из биологии, где естественный отбор оптимизирует генотип подобным образом. Поток информации при реализации ГА в задаче оптимизации представлен на рис.3.10.

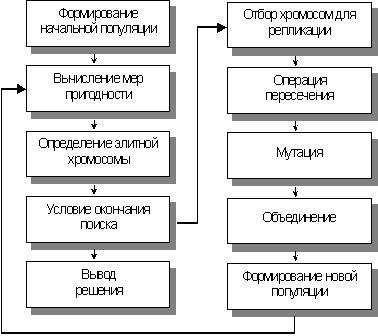
Рис.3.10.Обобщенная блок-схема генетического алгоритма

      В задачах синтеза ИС ГА позволяют находить на множестве возможных решений субоптимальные решения, которые передаются в качестве входной информации в ИНС, где обрабатываются наиболее подходящие решения. ИНС представляет собой высокопараллельную динамическую систему с топологией направленного графа, которая может получать информацию посредством реакции ее состояния на входные воздействия. Узлами в нейронной сети являются процессорные элементы и направленные каналы [9], [11]. Иначе говоря, ИНС - это сеть с конечным количеством элементов - аналогов нейронов с различными типами связей между слоями нейронов.

      Формальное представление модели нейрона отражает основные свойства биологического нейрона. На вход нейрона поступают n входных сигналов x_i (i=1,:,n). Выходом нейрона является сигнал y. Внутреннее состояние нейрона определяется через взвешенную сумму входных сигналов (синаптическая операция). Выходной сигнал нейрона определяется через сигмоидную функцию f  (соматическая операция) в виде

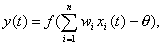        (3.30)

где 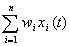=f(t) - входной суммарный сигнал; w_i - весовые коэфициенты; q -смещение модуля нейрона (параметра правдопобобия); t - время;  n -количество входов.

       Построение структуры ИНС при  решении задачи многокритериальной оптимизации ведется в такой последовательности:

·       На первом этапе путем кодирования структуры в виде хромосомы формируется исходная популяция сетей, удовлетворяющая некоторым заданным свойствам.

·       Производится обучение ИНС. Из популяции выбираются две родительские хромосомы, кодирующие те сети, которые удовлетворяют заданному правилу отбора.

·       Над выделенными хромосомами производится ряд генетических операций (инверсия, кроссовер, мутация), что приводит к изменению топологии соответствующих сетей, после чего они возвращаются в популяцию.

      Реализация логического вывода с  использованием концепции мягких вычислений представлена на рис.3.11.

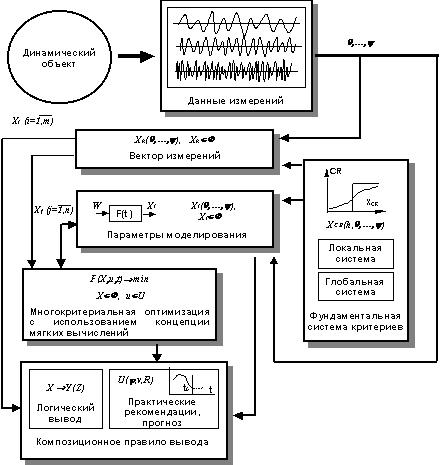
Рис.3.11. Поток информации при реализации логического вывода в задаче многокритериальной оптимизации

7.2. Мягкие измерения в интеллектуальных системах

       Концепция мягких вычислений оказывает растущее влияние на развитие ИС. Интегрирующие особенности мягких вычислений позволили разработать гибкие стратегии управления и комплексной оценки ситуаций, реализуемые в прикладных ИС.

Ниже рассмотрен нечеткий подход в рамках концепции мягких измерений при обработке информационных потоков в ИС поддержки принятия решений по управлению  подводными динамическими объектами [23]. Имеющиеся априорные сведения и данные гидроакустических наблюдений о эволюциях других динамических объектов в заданной акватории характеризуются значительным уровнем неточности и неопределенности. В такой ситуации элементы обрабатываемого в системе вектора измерений формируются по приближенным оценкам, полученным путем анализа измерительной информации (гидроакустические условия, уровень и характер шумов наблюдаемого объекта и т.п.). В зависимости от постулируемой степени трактовки понятий неточности и неопределенности применительно к отдельным данным, используемым для решения, может быть реализован детерминированный, вероятностный или нечеткий подход. Частным случаем последнего являются мягкие измерения  [4] ,[23].

          Модель мягких измерений предполагает описание измерений в терминах нечетких множеств. При этом неточности соответствует носитель нечеткого множества, а неопределенности - известная функция принадлежности. Поскольку алгоритмы принятия решений формируют результат на основе нечетких данных, а информационное пространство измерений может включать детерминированные и вероятностные характеристики, используется единое представление элементов вектора измерений в терминах нечетких множеств.

       В основу мягких измерений положены принципы байесовских интеллектуальных измерений, объединяющих в себе черты теоретико-вероятностного подхода, байесовского подхода и теории нечетких множеств. Фундаментальным понятием здесь является универсальная шкала, которая расширяет понятие традиционных шкал репрезентативной теории  измерений. Основная идея, позволяющая сформировать нечеткие измерения,  заключается в сопряжении лингвистической шкалы с основной шкалой за счет использования общего метрического носителя [23].

     Результатом мягких измерений являются выбранные на заданной шкале лингвистические значения оцениваемых в процессе наблюдения переменных. Реализация таких измерений заключается в проецировании всех возможных измерений на универсальное множество некоторой шкалы. Эта шкала определяется на известных элементах терм-множества лингвистических переменных и поставлена в соответствие конкретному измерению. Для преобразования информации используется операция фазификации. Эта операция позволяет четким значениям, полученным в результате непосредственных измерений или их вторичной обработки, приписать нечеткие множества как элементы соответствующих терм-множеств лингвистической переменной. Алгоритм нечеткого оценивания при реализации мягких вычислений описан в работе [22].

      Функционирование интеллектуальных измерительных средств основано на использовании заний о свойствах объекта,  условий и средств измерений, а также процедур метрологического анализа и синтеза. Повышение точности измерений и наличие способности к адаптации достигается за счет выбора значений (оптимизации) управляющих параметров измерительной процедуры, фильтрации аддитивных помех и коррекции погрешностей результатов измерений.  

7.3. Модель "мягких" измерений

Основой нечеткого подхода является описание измерений в терминах нечетких множеств (НМ). Тогда неточности соответствует носитель НМ, а неопределенности - известная функция принадлежности.

Учитывая, что алгоритмы принятия решений формируют результат на основе нечетких данных, а информационное пространство измерений может включать и детерминированные и вероятностные сведения, необходимо единое представление элементов вектора измерений в терминах НМ.

В случае четкого измерения параметра 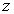 соответствующее ему НМ может быть представлено синглтоном 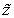 с функцией принадлежности

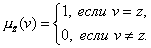         (3.31)

При вероятностном подходе, когда известна для 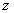 плотность распределения вероятности 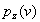, оценка функции принадлежности НМ 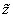 может быть получена на основе предложенного в работе [7] соотношения

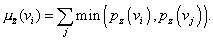  (3.32)

Следовательно, все измерения, используемые в нечетких системах принятия решений, представимы в терминах НМ.

Развитием нечеткого подхода является концепция <мягких> измерений. Она основана на принципах байесовских интеллектуальных измерений, объединяющих в себе черты теоретико-вероятностного подхода, байесовского подхода и теории нечетких множеств. Фундаментальным понятием является шкала, которая расширяет понятие традиционных шкал  репрезентативной теории измерений. К важному элементу рассматриваемых измерений относится шкалирование поступающей лингвистической информации. Основная идея заключается в сопряжении лингвистической шкалы с основной шкалой за счет использования общего метрического носителя, что позволяет формировать нечеткие измерения [6].

Результатом <мягких> измерений являются выбранные на заданной шкале лингвистические значения оцениваемых в процессе наблюдения переменных. Реализация таких измерений заключается в проецировании на универсальное множество, объединяющее все возможные значения измерения 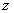, шкалы, которая определена на известных элементах терм-множества лингвистических переменных (ЛП), поставленной в соответствие конкретному 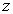. Тогда операция фазификации [8] позволяет четким значениям, полученным в результате непосредственных измерений или их вторичной обработки, приписать НМ, как элементы соответствующих терм-множеств ЛП.

Применим этот подход для нечеткого представления начальных оценок параметров движения наблюдаемого судна по данным от гидроакустической станции, работающий в пассивном режиме. Первичной информацией являются пеленг 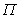, априорные данные о возможных скорости 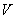 и курсовом угле 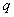, а также ориентировочная оценка дистанции .

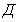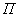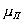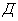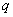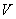Значение , как результат непосредственного измерения, представим НМ с функцией принадлежности , определяемой по формуле (3.31) или (3.32). С остальными параметрами движения судна связываются соответствующие ЛП: <ДИСТАНЦИЯ>, <КУРСОВОЙ УГОЛ> и <СКОРОСТЬ>. По результатам приближенного определения ,  и  на основе заданных ЛП формируются нечеткие оценки результатов "мягких" измерений.

Аналогичным образом выполняются измерения и в последующие дискретные моменты времени  

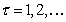
7.4. Алгоритм нечеткого оценивания

По известной на момент 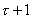 реализации мягких измерений, представленных вектором нечетких параметров 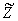, с учетом априорно известных элементов информационного пространства, относящихся к описанию динамики наблюдаемого судна, требуется оценить функции принадлежности параметров его движения.

Пусть движение судна описывается нечеткой линейной нестационарной системой

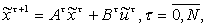     (3.33)

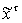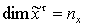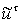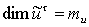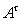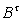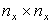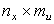где  - нечеткий вектор состояния объекта, ;  - известный нечеткий вектор управления, ; ,  - заданные матрицы размерности  и  соответственно.

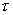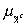На момент  известны вектор-функции принадлежности  и 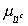. Предполагается, что 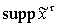 и 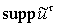 ограничены, соответственно, в 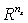 и .

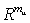Для 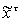 определим состояние системы (3.33) в момент времени 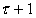, как 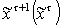 с вектор-функцией принадлежности .

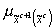Траектория системы (3.33) для любого начального состояния 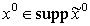 определяется, как последовательность НМ .

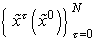Информация о реализациях выхода системы поступает от информационно-измери-тельной системы, модель наблюдения для которого описывается следующим уравнением

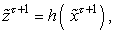               (3.34)

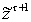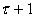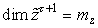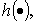где  - нечеткий вектор измерений на момент , ;  - известная вектор-функция.

Пусть в системе (3.33) на момент 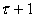 реализовались:

· некоторое неизвестное состояние 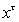 с функцией принадлежности ;

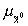· неизвестное управление ;

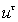· измерение .

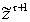Требуется описать НМ состояний 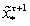, совместимых с выходом .

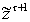Определим нечеткое множество потенциальной наблюдаемости 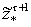 [9], как

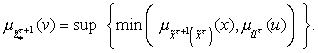
Множество 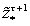 позволяет определить наличие уточняющего свойства в измерениях 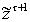. Эти свойства присутствуют при выполнении следующих условий:

· ;

· .

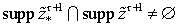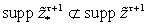Наличие измерений 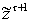 позволяет уточнить множество потенциальной наблюдаемости 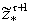. Реализованное множество наблюдаемости НМ 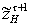 представляет собой пересечение множества потенциальной наблюдаемости 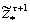 и множество измерений :

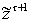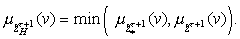  (3.35)

НМ 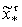 с функцией принадлежности 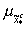 совместимо с выходом 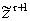, если выполняется условие 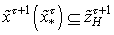, т.е. .

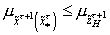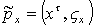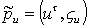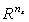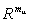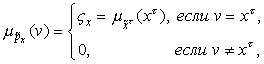Пусть  и  нечеткие точка в  и :

и 

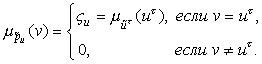
С учетом обозначений

, ,

, ,

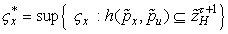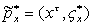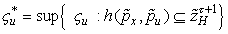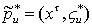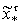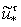решения  и  задачи апостериорного оценивания представляется в виде

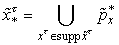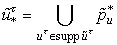,     (3.36)

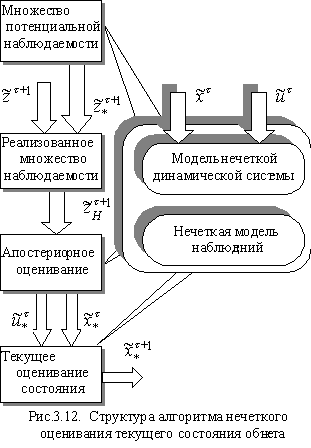
Формулы (6) позволяют решить задачу текущего оценивания нечеткого выхода системы (3) по результатам "мягких" измерений. Структура алгоритма приведена на рис. 3.11.

Четкие оценки формируются по результатам применения любого из известных методов дефазификации.

На основе разработанного алгоритма составлена компьютерная программа преобразования нечеткой информации с использованием концепции "мягких" вычислений. Эффективность программы продемонстрирована на базе измерительной информации, полученной во время натурных испытаний бортовой ИС анализа и прогноза мореходных качеств судов.

В судовых системах поддержки принятия решений учет неточности и неопределенности в процессе измерений возможен на основе реализации положений концепции <мягких> измерений. Эта концепция предполагает проецирование результатов измерений или их вторичной обработки на шкалу, объединяющую лингвистическую и основную шкалы с общим метрическим носителем. Полученные результаты позволяют решать задачу нечеткого оценивания текущих параметров движения судна, информация о которых обеспечивает повышение эффективности организации маневрирования в сложных ситуациях.

Управление процессом обработки информации, реализующим концепцию "мягких" измерений, осуществляется с помощью нечетких логических операторов формализованной системы знаний. Интерпретация ситуаций и сценариев их развития в рамках изложенного подхода позволяет рационально организовать выявление и свертку информации о характеристиках внешней среды и более строгого подойти к решению проблемы безопасности судовождения.

Таким образом, разработанный подход создает методологическую базу для преобразования информации в системах поддержки принятия решений по обеспечению маневрирования судов и плавучих технических средств освоения океана в сложных гидрометеорологических условиях