|
Проблема
адекватности математических
моделей имеет непосредственное
отношение к построению базы знаний
и эффективности функционирования
ИС в процессе эксплуатации.
Выдаваемые системой практические
рекомендации в значительной
степени определяются надежностью
информации, получаемой в результате
математического моделирования [1].
Использование алгоритмов
приближенных рассуждений для
процедур принятия решений при
логическом выводе в нечетких
системах привело к необходимости
исследования и устранения
противоречий в выводах с помощью
диалоговых процедур о состоянии
динамической системы. В основу этих
процедур может быть положен анализ
состояния системы на фазовой
плоскости - формирование фазового
портрета динамической системы по
фазовым координатам ее движения. В
общем случае динамика системы
порождает устойчивые формально-логические
структуры как результат действия
синергетических процессов. Анализ
сформированных логических структур
проводится на базе активных
диалоговых процедур. Сохранение
основных свойств качественного
описания исследуемой системы и
эффективность алгоритма
приближенных рассуждений
проверяются с помощью
имитационного моделирования.
Ниже
обсуждается проблема адекватности
математических моделей плавучих
динамических объектов. Рассмотрены
различные подходы к определению
нелинейной пространственной
функции, характеризующей
восстанавливающую компоненту при
бортовой качке, указаны пути
математического описания
физических картин динамики
взаимодействия объекта с внешней
средой, дается характеристика
особенностей вычислительной
технологии и интерпретации
результатов моделирования.
Приведены примеры численных и
экспериментальных оценок
исследуемых явлений
В работах, посвященных
исследованию динамик и плавучих
объектов на волнении, используются
приближенные методы анализа
математических моделей,
описывающих сложное
гидроаэродинамическое
взаимодействие объекта с внешней
средой. Существенная нелинейность и
вероятностная основа таких моделей,
невозможность строгого учета
компонент вектора состояния ставят
перед исследователями сложные
проблемы анализа ситуации и
вычислительной технологии,
преодоление которых неизменно
связано со специфическими
трудностями и требует большого
труда и фантазии. Современные
работы такого направления
выполняются на базе обобщения идей
и методов на все более абстрактные
ситуации, требующие новых
разработок и конструкций.
Используемые подходы иногда
создают видимость исчерпывающего
решения задачи, тогда как проблема
состоит не в возможности получения
приближенного решения, в
фактической эффективности
предлагаемого алгоритма.
Видимая тривиальность
вычислительных задач способствует
появлению работ. Не связанных с
экспериментальной проверкой
полученных данных. В отдельных
случаях даже не содержится
подробного алгоритма и численного
материала, позволяющего судить об
эффективности метода и оценке
полученного результата с позиций
вычислительной математики.
Искусство анализа и квалификация
результата как близкого к
экспериментальным данным -
необходимый элемент
исследовательской работы.
Трудности решения задач
динамики плавучих объектов на
волнении состоят в том, что
сравнительно малая погрешность в
исходных данных при
вычислении компонент
математических моделей связана с
большой неопределенностью в
решении Такая ситуация особенно
недопустима в задачах оценки потери
устойчивости (опрокидывание). Так
как решение представляет собой
информацию о важнейшем мореходном
качестве, погрешность при оценке
которого на практике может привести
к тяжелым последствиям.
Приближенными решениями задач
динамики занимаются многие
специалисты. Каждый из них имеет
свою точку зрения на постановку
данных задач, характер
встречающихся трудностей,
объяснение различных ситуаций в
процессе решения и содержательного
анализа результатов. Не всегда
соглашаясь с имеющимися выводами и
объяснениями феномена, выявленного
в процессе решения, автор считает
необходимым рассмотреть вопрос об
адекватности математических
моделей плавучих динамических
объектов на волнении .
Пусть имеется математическая
модель, характеризующая поведение
плавучего динамического объекта на
волнении под воздействием внешних
возмущений:
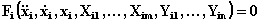 (3.18) (3.18)
где F(·) -
нелинейные функции;
xi - линейные и
угловые перемещения;
Xij - параметры,
характеризующие рассматриваемый
объект как динамическую систему (инерционные,
демпфирующие и восстанавливающие
компоненты); Yij
- возмущающие силы и
моменты.
Наиболее сложной
функцией в системе (3.18) является
восстанавливающая компонента,
входящая в дифференциальное
уравнение вращения судна
относительно продольной
центральной оси. Восстанавливающая
компонента характеризуется
существенной нелинейностью,
сложностью и многозначностью.
Непрерывно изменяясь во времени и
пространстве, эта функция в
значительной степени определяет
физические картины
взаимодействия ДО с внешней средой.
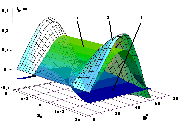
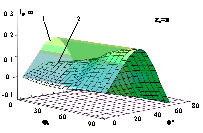
Для общего представления о виде
рассматриваемой нелинейной функции
в задаче о динамическом наклонении
плавучего ДО под воздействием
внешних возмущений, на рис.3.6
приведена реализация
поверхности, характеризующей
восстанавливающую компоненту при
различных значениях определяющих
параметров.
|
|
|
|
|
|
|
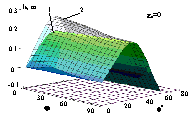
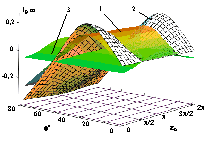
Рис.3.6.
Нелинейная функция, описывающая восстанавливающую компоненту
|
Математическое
описание этой поверхности
представляется в виде полинома,
зависящего от параметров морского
волнения, элементов ДО,
скорости его движения и
ориентации относительно
направления бега волн:
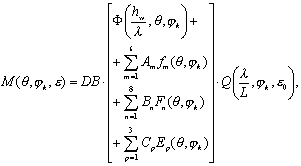 (3.19)
(3.19)
Здесь Ф, fm, Fn,
Ep - нелинейные функции,
учитывающие влияние параметров
волнения (длины l
и высоты hw
волны), относительной скорости (числа
Фруда) и элементов формы корпуса ДО
при различных значениях угла крена q, курсового угла jk
и фазы e, характеризующей
положение судна относительно волны;
D,B - водоизмещение и ширина ДО.
Наличие
качки большой амплитуды плавучего
динамического объекта при
интенсивных динамических нагрузках
включает в действие новую
физическую связь, <дремавшую> в
случае слабых возмущений. В
результате происходит резкое
изменение картины взаимодействия
динамического объекта с внешней
средой. Качественные исследования
нелинейных динамических систем при
различном уровне внешних
возмущений свидетельствуют о
сложной эволюции
фазовых траекторий, нарушающих
симметрию фазового пространства и
приводящих к образованию
аттракторных множеств. Особенно
сложными оказываются случаи,
характеризующие динамику
бистабильной и трехстабильной
системы (см. ниже рис.3.8). На разных
стадиях своего развития
исследуемые фазовые портреты
напоминают поведение
самоорганизующихся систем. Процесс
самоорганизации заключается в
переходе системы из одного
стабильного состояния в другое, При
этом фазовые траектории как бы <втягиваются>
в тот или иной аттрактор. При одних
состояниях системы возникают
аттракторы типа <предельный цикл>,
а при других состояния равновесия
оказываются зависимыми от времени.
Учет этих особенностей при
формализации знаний с
использованием встроенных процедур, основанных на
стандартных математических методах,
представляет собой
достаточно сложную задачу
анализа и интерпретации
результатов математического
моделирования.
Результаты исследования
позволяют выделить различные
сценарии образования аттракторных
множеств. При определенном уровне
внешних возмущений и параметров
системы может происходить слияние
двух и более состояний равновесия,
часть из которых устойчива и часть
неустойчива. Этот феномен связан с
качественными изменениями в
поведении системы, когда система
скачком переходит из одного режима
движения в другой. Наличие скачка (катастрофы)
может иметь и более сложный
характер в зависимости от
параметров системы. В отдельных
случаях возможно исчезновение <предельного
цикла> и переход системы либо в
устойчивый <предельный
цикл> . либо в более сложный
аттрактор. Вычислительные
эксперименты с математической
моделью плавучих динамических объектов
показывают, что наличие сильной
периодической составляющей
восстанавливающей компоненты
приводит к более сложной топологии
фазового пространства. При этом
частота исходного периодического
движения оказывается близкой к
доминирующей частоте в спектре
аттрактора. Анализ результатов
моделирования также указывает на
существование общих принципов и
закономерностей преобразования
информации в системах со сложной
динамикой. На этой
основе могут быть построены
различные математические структуры
(одномерные и многомерные
отображения), реализующие процессы
обработки информации. Важным
результатом исследования
нелинейной динамики плавучего
объекта, является практическая
невозможность использования
методов статистической
линеаризации, широко применяемых
при анализе нелинейных систем.
Сопоставление топологии фазового
пространства для нелинейной и
линеаризованной
математической модели
свидетельствует о практической
невозможности сохранения фазовых
потоков, порождающих странные
аттракторы и детерминированный
хаос, в линеаризованных системах [1].
Обозначим через
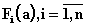 , критерий адекватности,
определяемый из анализа
математической модели с учетом
описываемых видов движения и
представляющий собой либо функцию
от параметров
, критерий адекватности,
определяемый из анализа
математической модели с учетом
описываемых видов движения и
представляющий собой либо функцию
от параметров
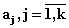 , либо функционалы кривых
соответствующих дифференциальных
уравнений. Коэффициенты модели aj,
удовлетворяющие заданным
параметрическим, функциональным и
критериальным ограничениям,
образуют допустимую область Ea
в пространстве критериев F(Ea).
Задавая точность аппроксимации
параметров aj в виде
, либо функционалы кривых
соответствующих дифференциальных
уравнений. Коэффициенты модели aj,
удовлетворяющие заданным
параметрическим, функциональным и
критериальным ограничениям,
образуют допустимую область Ea
в пространстве критериев F(Ea).
Задавая точность аппроксимации
параметров aj в виде
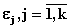 и точность
критериев
и точность
критериев
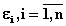 , можно представить критерий
близости (адекватности) данных
математического моделирования
физическому эксперименту
, можно представить критерий
близости (адекватности) данных
математического моделирования
физическому эксперименту
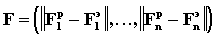 , (3.20)
, (3.20)
где индекс
обозначает расчет, а <э> -
эксперимент.
Для определения с
заданной точностью параметров
математической модели динамики
судна на волнении с принятыми
значениями критериев необходима
аппроксимация области Ea. Это
достигается за счет нахождения
значений aj таких, что
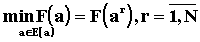 , (3.21)
, (3.21)
при условии,
определяющем допустимую область Ea,
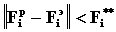 , (3.22)
, (3.22)
если задана граница
вариаций параметров
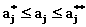 , где N - число экспериментов,
, где N - число экспериментов,
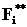 -
допустимые критериальные
ограничения (уровень адекватности),
устанавливаемые в процессе диалога
исследователя с компьютером с
учетом точности данных физического
моделирования.
-
допустимые критериальные
ограничения (уровень адекватности),
устанавливаемые в процессе диалога
исследователя с компьютером с
учетом точности данных физического
моделирования.
Конкретизация
общих зависимостей (3.20)-(3.22) при
построении адекватной модели в
ИС реального времени
приводит к следующей задаче.
Представим
математическую модель (3.18) как
локальное дискретное
преобразование
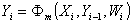 ,
,
где Yi
- моделируемое состояние
динамического объекта в i-й момент
времени. (Yi-1 - тоже, но в момент времени i-1; Xi
и
Wi - состояние внешней среды и
внутреннее состояние объекта в i-й
момент времени.
Введем
понятие вектора исходных данных
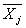 и вектора
поведения модели
и вектора
поведения модели
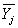 в j-м
прогоне
в j-м
прогоне
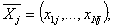
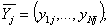
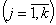 ,
,
где N -
объем одного прогона модели; k
- число прогонов.
В качестве критериев
адекватности могут быть
использованы допустимые
расхождения теоретических и
экспериментальных данных при
оценке амплитудных значений
различных видов качки (детерминированные
или вероятностные отношения для
угловых и линейных перемещений,
скоростей и ускорений), а также
ограничения, накладываемые на
расхождение временных и фазовых
траекторий при оценке поведения
динамической системы, условия
проверки принадлежности выборочных
данных эмпирическим законам
распределений (законы Гаусса, Рэлея,
Вейбулла и др.).
Оценка адекватности
усложняется для математических
моделей большой размерности (например,
при исследовании наклонения судна с
учетом поперечно-горизонтальной и
вертикальной качки). В этом случае
содержательность задачи
восстановления параметров
определяется не только структурой
модели, но и принятыми критериями
близости теоретических и
экспериментальных данных, а также
степенью полноты вектора критериев.
В задачах оценки поведения судна в
рассматриваемой ситуации
имитационная модель представлялась
в виде:
Фi,mÎ{FM, P(
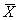 )},
)},
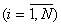 , (3.23)
, (3.23)
где
FM
- оператор, отображающий множество
ситуаций {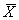 }
в множество поведений { }
в множество поведений {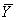 }
локальной модели Фm;
i
- рассматриваемый момент времени; P( }
локальной модели Фm;
i
- рассматриваемый момент времени; P(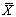 )
- вероятностное распределение,
характеризующее множество исходных
данных, поступающих от
измерительной системы. )
- вероятностное распределение,
характеризующее множество исходных
данных, поступающих от
измерительной системы.
Множества
{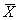 }
и { }
и {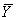 }
в j-м решении (прогоне) связаны
соотношением: }
в j-м решении (прогоне) связаны
соотношением:
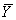 = FM( = FM(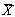 ), ),
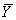 ={Yj}, ={Yj},
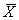 ={Xj}, ={Xj},
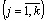 .
.
Условие
адекватности определяется как
YÎS "cÎCm, (3.24)
где S - область, ограничивающая поведение
модели; Cm
-
цели моделирования.
Процедура
построения модели связана с
решением проблемы выбора класса
модели и области S. В
качестве меры отклонения поведения
модели используется функция штрафа
(неадекватности):
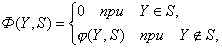 (3.25)
(3.25)
где j(Y,S)
- функция, определяющая степень
неадекватности.
Разработанная
с учетом этих требований
имитационная модель позволяет
обеспечить контроль и прогноз
развития экстремальной ситуации,
связанной с ухудшением
характеристик динамического
объекта.
Понятие адекватности связано с
другой очень важной особенностью
нелинейных динамических систем -
грубостью их математических
моделей. Использование этого
понятия вызвано тем, что любая
адекватная модель отражает
исследуемое явление лишь с
некоторой приближенностью,
практически никогда не описывая ее
абсолютно точно. Поэтому при
анализе математических моделей
необходимо получать данные, которые
не испытывали бы заметной
зависимости от неточности
моделирования, т.е. были бы
достаточно инвариантными по
отношению к этим неточностям. Таким
образом, понятие грубости
свидетельствует о том, что
результаты исследования модели и
характер ее динамики должны
испытывать достаточно малые
изменения при сравнительно
небольших вариациях структуры
модели [1], [12].
Улучшение математических
моделей динамики плавучих объектов
на волнении способствует
совершенствование теоретической и
экспериментальной базы
гидроаэродинамических
исследований, использование
эффективных методов обработки и
анализа результатов эксперимента.
Важное значение для повышения
адекватности имеет разработка
надежных способов определения
компонент математических моделей с
учетом искажений, вносимых
движущимся объектом в структуру
волны (интерференция и дифракция
волн, изменение поля давлений),
более полного описания
пространственной и временной
структуры ветровых потоков и
демпфирования при входе палубы,
фальшборта и надстройки в воду.
В качестве модели обработки
данных математического и
физического моделирования при
оценке адекватности можно
рассматривать информационную
модель, представленную на рис.3.7.
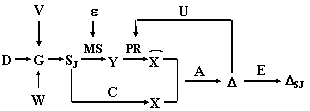
Рис.3.7.
Граф-схема информационной модели
взаимодействия судна с внешней
средой: D -
динамический объект (судно); V,
W - внешняя среда (ветер, волнение); G
-модель генерации ситуаций; Sj
- конкретная (J) ситуация; MS -
измерительная система, содержащая
приборы для наблюдения и измерения
свойств изучаемого объекта (кинематических
и динамических характеристик) в J-й
ситуации; e
- погрешность измерения; Y -
результаты наблюдений; PR -
процессор, осуществляющий
преобразование измерительной и
априорной информации с помощью
методов математического и
лингвистического моделирования;
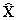 -
результаты имитационного
моделирования (новые знания о
динамике взаимодействия); C - модель
взаимодействия (целевой оператор)
формирующий достоверную оценку X (результаты
физического моделирования); A -
адекватор, сравнивающий
-
результаты имитационного
моделирования (новые знания о
динамике взаимодействия); C - модель
взаимодействия (целевой оператор)
формирующий достоверную оценку X (результаты
физического моделирования); A -
адекватор, сравнивающий
 и X и выдающий
оценку адекватности D
полученных значений X; U -
управление, корректирующее
лингвистическую модель и
настраивающее коэффициенты
математической модели, а при
необходимости - выбирающее более
подходящее математическое описание;
E - оператор, дающий максимально
возможную оценку адекватности DSJ.
и X и выдающий
оценку адекватности D
полученных значений X; U -
управление, корректирующее
лингвистическую модель и
настраивающее коэффициенты
математической модели, а при
необходимости - выбирающее более
подходящее математическое описание;
E - оператор, дающий максимально
возможную оценку адекватности DSJ.
Проблема адекватности нечетких
моделей реальному объекту в задачах
интерпретации при нечетком
моделировании динамических
процессов связана с разработкой
специальных критериев адекватности.
Обычно в исходной модели нечеткие
множества представляются
параметрически в виде R-L
чисел. Они задаются
субъективно и достаточно
приближенно, а затем в процессе
экспериментирования при обучении
на реальной ситуации
осуществляется их настройка,
доводка и коррекция. Используемые
при этом логические операции
облегчают моделирование и поиск
решения задачи.
Наибольшее влияние на поведение
исследуемой динамической системы
оказывает восстанавливающая
компонента, представляющая собой
существенно нелинейную
функцию, непрерывно
изменяющуюся во времени и
пространстве. Вопрос о надежной
оценке этой функции особенно
актуален при исследовании динамики
объекта при различных курсовых
углах на попутном волнении. В этом
случае в наибольшей степени
проявляется влияние интерференции
корабельных и набегающих волн и
результаты теоретических оценок, не
учитывающих этого фактора,
отклоняются от экспериментальных
данных. Особенно резкое расхождение
данных наблюдается при высоких
числах Фруда для динамических
объектов малых удлинений (малое
отношение длины к ширине объекта).
Здесь величина расхождения
достигает существенных значений в
зависимости от соотношений главных
размерений и коэффициентов полноты
формы корпуса динамического
объекта. Это расхождение настолько
велико, что практически приводит к
нарушению требований адекватности
в широком диапазоне скоростного
режима и параметров ветроволновых
возмущений.
Стремясь улучшить
математическое описание
исследуемого процесса,
экспериментатор должен учитывать
ограничения, накладываемые на
модель: она не должна быть слишком
простой для того, чтобы не утратить
возможности правильного
отображения динамики явления, но и
не слишком сложной, загроможденной
второстепенными несущественными
деталями.
В практике исследований
поведения плавучих динамических
объектов на волнении выработан
определенный тип математических
моделей, которые в зависимости от
ориентации объекта относительно
генерального направления бега волн
описывают изучаемые явления с
достаточной для практических целей
точностью. Как показывает сравнение
данных математического
моделирования с результатами
физического эксперимента, характер
колебательного движения при крене и опрокидывании
сохраняется приблизительно
одинаковым, а наблюдаемое
расхождение кривых связано с
достоверностью оценки компонент
при построении математических
моделей (особенно демпфирующей и
восстанавливающей компонент). В
зависимости от исходных данных
расхождение теоретических и
экспериментальных кривых может
достигать существенных величин, как
и при оценке восстанавливающей
компоненты. Однако при
корректном определении
указанных компонент удается
получить результаты, погрешность
которых не превышает 10-15%, т.е. лежит
в пределах обычной погрешности
эксперимента по исследованию
динамики плавучего объекта на
волнении с помощью самоходных
радиоуправляемых моделей.
Особую тщательность следует
проявлять при описании восстанавливающей
компоненты в сложных ситуациях (движение
плавучего объекта с различными
курсовыми углами на попутном и
встречном волнении, динамика
аварийного объекта с затопленными
отсеками). В этих условиях
сравнительно малое расхождение в
исходных данных может привести к
принципиально новой интерпретации
исследуемого явления. В качестве
примера, свидетельствующего о
резком расхождении траекторий
движения динамической системы при
малом различии
исходных данных, сопоставим фазовые
портреты для одной и той же
динамической системы, описанной с
помощью детерминированной модели,
описывающей бортовую качку под
воздействием гармонического
возмущения. Будем считать
инерционно-демпфирующие компоненты
в рассматриваемых случаях
одинаковыми (демпфирование примем в
виде линейной функции угловой
скорости), а восстанавливающий
момент M(q,t) опишем близкими
по виду нелинейными функциями
m1(q,t)=[M0(q,t)+DM(q,t)]/(Jx+mqq); (3.26)
m2(q,t)=M0*(q,t)/(Jx+mqq),
(3.27)
где M0(q,t) и
M0*(q,t)
различаются линейными членами, а DM(q,t)
- приращение восстанавливающего
момента, обусловленное влиянием
надстроек при больших углах крена; Jx+mqq
- момент инерции массы судна вместе
с присоединенной массой воды
относительно продольной
центральной оси.
Как
показывают результаты численного
анализа (рис.3.8), незначительное
расхождение в описании
восстанавливающей компоненты
математической модели (полиномиальная
аппроксимация с различными
линейными членами) при водит к
принципиальным различиям в
картинах полведения
рассматриваемой динамической
системы на фазовой плоскости. В
первом случае (рис.3.8А) фазовый
портрет динамики объекта содержит
пять особых точек: два седла
S1 и S2
и три устойчивых фокуса, лежащих
на одной прямой. Центральный фокус
расположен в начале координат, а
двум другим соответствуют
фиксированные колебания с
различной фазой. Во втором случае (рис.3.8В)
устойчивая точка, соответствующая
началу координат на фазовой
плоскости, становится седловой
точкой, а фазовые траектории
приобретают совершенно иной вид. В
результате исследуемая
динамическая система за счет малого
различия исходных данных при
описании восстанавливающей
компоненты из трехстабильной
превратилась в бистабильную
систему с принципиально новой
топологией фазового пространства.
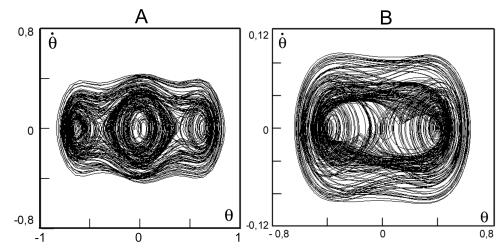
Рис.3.8
Фазовые портреты трехстабильной (А)
и бистабильной (Б) динамической
системы, характеризующие поведение
аварийного плавучего ДО в
экстремальной ситуации
При оценке адекватности
математических моделей следует
учитывать особенности
вычислительной технологии.
Негативная тенденция трактовать
вычислительную математику как
умение пользоваться набором
стандартных программ решения
различных задач создает ложное
впечатление об их неограниченных
возможностях. Заявление об удачном
и надежном решении сложных задач
относительно простыми средствами
не всегда соответствует
действительности. Ведь речь идет о
задачах с заранее неизвестным
ответом. Такой ответ может быть
получен только в тестовых задачах. В
отдельных случаях его можно
получить в процессе анализа
численных результатов. Большую
пользу при этом могут оказать
данные, полученные с помощью других
численных методов. Доверять решению
в сложных ситуациях, не поддающихся
строгой проверке, можно, только если
метод дает хорошие результаты в
задачах, где решение может быть
строго проанализировано. Выход из
этой тупиковой ситуации следует
искать в совершенствовании самого
подхода и путей его реализации
наряду с гарантией необходимой
точности методов численного
интегрирования. Критическое
отношение к полученным данным,
сомнение в их правильности,
искусство анализа и интерпретации
результата - важный арсенал
вычислительной работы
Громоздкость задач динамики,
связанных с использованием
достаточно строгих методов
исследования нелинейных
стохастических систем (метод Монте-Карло,
уравнение Фоккера-Планка-Колмогорова),
выдвигает наряду с отмеченными
особенностями и проблему машинного
времени. Реализация алгоритма на
компьютере в этом случае неизбежно
связана с с большим объемом
вычислений. Желание получить
решение с заданной точностью ценой
конечного числа операций может
оказаться совершенно
необоснованным из-за невыполнения
предположений, принятых в
доказательстве, наряду с
требованиями современной
вычислительной математики, а также
катастрофическим объемом
вычислений. Немало трудностей
встречается и при сведении задачи
динамики к краевой задаче. Хорошая
точность в этом случае достигается
за счет соблюдения общих требований
к анализу краевых задач, включая
сходимость численного метода в
окрестности решения, нарушение
единственности решения,
неоднозначность отображения и
выбор начального приближения.
Нарушение этих условий может лишить
процедуру анализа краевой задачи
шансов на успех [20].
Проверка адекватности
математических моделей плавучих
динамических объектов на волнении
осуществляется как в процессе
разработки базы знаний, так и при
функционировании ИС на борту
динамического объекта. На этапе
разработки программного
обеспечения процедурной компоненты
эта операция основана на
сопоставлении данных
математического моделирования с
материалами физического
эксперимента, а также использовании
регрессионных зависимостей,
адекватность которых проверялась
при их построении. В процессе
эксплуатации ИС происходит
корректировка математических
моделей на базе поступающей
измерительной информации о
фактическом взаимодействии
динамического объекта с внешней
средой. Математические модели
прогноза динамических
характеристик судна в этом случае
непрерывно <подстраиваются> с
помощью адаптивной компоненты.
Реализация разработанного
подхода к оценке математических
моделей в ИС обеспечения
безопасности мореплавания
осуществляется с использованием
материалов физического
эксперимента. При этом исходные
модели оцениваются по данным
физического моделирования, а
рабочие модели - на основании
результатов натурных измерений в
процессе адаптации системы на борту
исследуемого динамического объекта.
|