4. Планирование эксперимента при функционировании интеллектуальных систем

Содержательный анализ проблем моделирования, определяемых соотношением между реальным экспериментом, модельным экспериментом и теорией, свидетельствует о постоянном внимании исследователей к поиску возможных стратегий моделирования с учетом особенностей исходной информации. Развитие этих подходов связано с применением ИС и стремительно растущей производительности вычислительных средств.

Формальные процедуры, лежащие в основе функционирования ИС, предполагают широкое использование измерительной информации и методов математического моделирования. Решение прикладных задач анализа и прогноза поведения динамического объекта в ИС ведется статистическими методами с привлечением теории планирования эксперимента. Информация, получаемая от датчиков динамических измерений в процессе нормальной эксплуатации объекта представляет собой данные пассивного эксперимента. Активный эксперимент используется только на этапе тестирования и адаптации ИС. При использовании данных активного эксперимента проблема выбора наилучшего математического описания может быть решена классическими методами планирования. В случае пассивного эксперимента эта проблема требует специальных подходов, учитывающих адекватность описания, дисперсию оценок и вычислительные трудности из-за вырождения информационной матрицы [1]. Для обратных задач математической физики в ИС типичными являются ситуации, когда наблюдение реализуется не "в точке", а "на функционале", что приводит к задачам с бесконечной областью планирования.

Рассмотрим анализ подходов к планированию эксперимента и поиску эффективных процедур обработки информации на основе разработки сложных ИС, функционирующих в реальном масштабе времени [1], [16].

4.1. Особенности планирования эксперимента

Возникающие при практическом использовании ИС задачи планирования эксперимента часто выходят за рамки классического подхода и требуют специального обобщения с учетом особенностей рассматриваемых проблем. В реальных измерениях ресурсы могут быть существенно ограничены, а априорная информация недостаточна для несмещенной оценки функции регрессии. В этих условиях приходится считаться не только со случайной ошибкой приближения, но и с систематической ошибкой, вызванной неадекватностью принятой модели. Выбор пространства, в котором ищется оценка, приходится осуществлять совместно с планом эксперимента и методом оценивания.

Понимая под планом эксперимента x вероятностную меру на области планирования U с конечным носителем sup x = {hÎU, x(h)¹0} и обозначая через H₁ конечномерное подпространство некоторого пространства H (H₁ÍH), которому принадлежит функция регрессии, будем считать, что по условиям реального эксперимента могут быть использованы только планы из допустимого множества

J_N := {x ÎJ_N : card(sup x) £ n},

где n - число, характеризующее ограниченность ресурсов.

Выбор пространства оценивания H₁=H_x и оператора оценивания S=S_x обеспечивает при фиксированном плане xÎJ_N нахождение наилучшего в метрике пространства H приближения 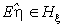 к произвольному элементу h из H. При этом пространство оценивания H_x должно обеспечивать построение оценки 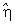 неизвестного элемента hÎH.

Задача выбора процедуры p=(x, H₁, S) восстановления h из H на множестве допустимых процедур p является двухкритериальной. В этих условиях поиск оптимальной процедуры p^* удобно вести на основе решения задачи оптимизации с приоритетом, учитывающим систематическую ошибку.

p^* = Arg inf B_g(p),                (3.1)

где g - вероятностная мера, используемая для осреднения систематической ошибки B(x, H₁, S)

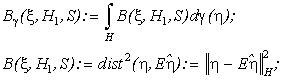
S - оператор, с помощью которого производится оценка 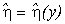 неизвестного элемента hÎH.

Для характеристики случайной ошибки используют функционал F(x,H₁,S) от корреляционного оператора оценки 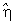 (определитель 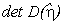, след tr 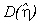или другие критерии), и тогда

                 (3.2)

где - множество процедур p^*, являющихся решением задачи (3.1).

Задача (3.2) на множестве процедур

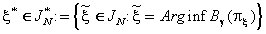
рассматривается в предположении, что носитель плана sup x определен однозначно из решения задачи (1), но имеется свобода в выборе весов наблюдений P_j (j = 1, m). Это позволяет минимизировать случайную ошибку при следующих условиях

x^*(P):=(h ,..., h ,P₁,...,P_m);

P^*=Arg inf F[D_x*(P)],

где P := {PÎR^m; P_j > 0,  j=1,m, S };

D_x*(P)- корреляционный оператор, определяемый как D_x = 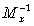 (M_x - информационный оператор).

В прикладных задачах планирования эксперимента важное значение приобретает интерпретация таких свойств как ортогональность и ротатабельность. При равноточных измерениях эти свойства приводят к независимости коэффициентов регрессии (их одинаковой точности), что принципиально в поисковых процедурах Бокса-Уилсона при экстремальном планировании.

4.2. Выбор оптимальных условий эксперимента

Задача выбора оптимальных условий эксперимента в ИС определяет надежную оценку характеристик динамического объекта и параметров внешней среды и связана с построением нормированного дискретного плана для динамического объекта, развивающегося во времени и пространстве. Пассивная стратегия планирования такого эксперимента характеризуется тем, что объект функционирует в режиме нормальной эксплуатации. ИС на основе анализа ситуации выбирает моменты времени и координаты точек, в которых следует производить измерения. Выполнив серию опытов при некоторых фиксированных значениях исследуемого фактора в различные моменты времени и имея модель системы, можно подсчитать нормированную информационную матрицу [2]

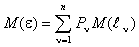     (3.3)

для дискретного плана эксперимента

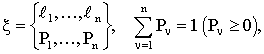     (3.4)

где P_n - веса наблюдений.

Синтез D-оптимальных планов измерений осуществляется на основе итерационной процедуры с использованием функции

d(l,x)=sup[M^-1(x)M(l)]        (3.5)

Особым случаем идентификации динамических систем является планирование измерений в частотной области. Управление процессом измерений на основании методов планирования эксперимента позволяет свести задачу к поиску дискретного оптимального плана

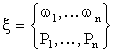       (3.6)

с нормированной информационной матрицей

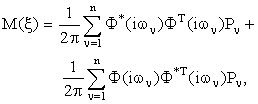    (3.7)

где w_n - частота спектрального разложения стационарной случайной функции (входного процесса); P_n - ординаты непрерывного спектра этой функции; звездочкой (*) помечены комплексно сопряженные частотные характеристики.

При однократных наблюдениях вместо (3.7) имеем

M(w)=1/2p [F^*(iw)F^T(iw)+F(iw)F^*T(iw)]      (3.8)

Выражения (3.6)-(3.8) позволяют построить функцию

d(w,x)=sup[M^-1(x)M(w)],    (3.9)

лежащую в основе алгоритмов синтеза D-оптимальных планов эксперимента.

Интервал, на котором определена вероятностная мера, порожденная нормированной спектральной плотностью, характеризуется выражением

W_w = [-w_k, +w_k]     (3.10)

где [-w_k, +w_k] - диапазон частот, определяющий полосу пропускания исследуемого динамического объекта.

4.3. Оптимальная структура моделей

В условиях эксплуатации ИС функционируют в реальном масштабе времени, и значительное усложнение используемых математических моделей приводит к громоздким алгоритмам преобразования измерительной информации, затрудняющим процедуру адаптации на выделенном временном интервале.

Рассмотрим в качестве исходной математической модели зависимость

Y = X b + e;          (3.11)

E(e) = 0, cov(e) = s² I

где X - (N´k) - матрица наблюдений регрессоров x_j; b - вектор-столбец значений неизвестных коэффициентов размерности (k+1); e - вектор-столбец значений регрессионной ошибки размерности (k+1); Y - вектор-столбец выходной переменной; E - оператор математического ожидания; I - единичная матрица; N - объем выборки; k - число регрессоров; s² - дисперсия воспроизводимости.

Точность прогноза модели (3.11) определяется дисперсией ошибки предсказания. Для (N+1) наблюдения по адекватной модели эта дисперсия равна

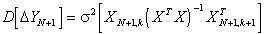    (3.12)

где X_N+1,k - вектор-строка размерности (1´k).

Для сопоставления дисперсий моделей с <недобором> и <перебором> регрессионных переменных относительно истинной зависимости выражение (3.12) преобразуется к виду:

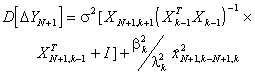   (3.13)

где l_k - параметр нецентральности t-распределения с N-k степенями свободы

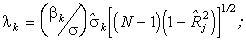
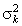- выборочная дисперсия переменной x_k; 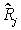 - выборочный коэффициент множественной корреляции переменной x_k с остальными независимыми переменными x₁, ... , x_k-1, вычисленный по данным матрицы наблюдений X.

Дисперсия ошибки прогноза с "недобором" и "перебором" будет равна

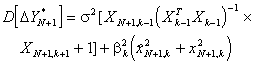         (3.14)

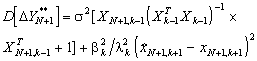         (3.15)

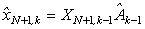Здесь b_k - значение коэффициента при k-ой неучтенной переменной x_k; x_N+1,k - значение (N+1)-го наблюдения k-ой переменной;  - регрессия переменной 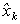 на остальные переменные 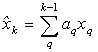;  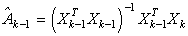- вектор-столбец коэффициентов размерности (k-1)´1.

На практике приходится избегать переусложнения модели за счет включения дополнительных регрессоров, так как

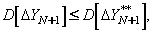
что следует из сопоставления (3.12) и (3.15). При этом равенство дисперсий достигается только при .

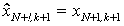Процедура построения оптимальной регрессионной структуры была протестирована при обработке данных физического эксперимента, проведенного во время натурных испытаний ИС на морских судах различного назначения (табл.3.1)

Выбор наилучшего уравнения поверхности отклика может быть произведен также с использованием базисных функций [3]. В этом случае используют модель вида

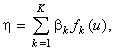
где b_k - k-й коэффициент регрессии; f_k(u) - k-ая базисная функция (f₁(u)º1); u = (u₁, ..., u_M)^T - вектор факторов пассивного эксперимента; M - число факторов; K - общее число слагаемых. При этом факторы кодированы, а модель наблюдения имеет вид Y = h + e.

Таблица 3.1. Характеристики различных способов формирования регрессионной структуры.

1 - полная адекватная модель; 2 - модель с "недобором"; 3 - модель с "перебором"

S₀ - остаточная сумма квадратов

Системный анализ задачи выбора наилучшей полиномиальной регрессии позволяет сформулировать подход к определению степени m_opt алгебраического многочлена P_m(c,x), наиболее точно аппроксимирующего заданную экспериментальную зависимость {y_n, x_n}. Суть его состоит в дополнении классического метода (выбор в качестве m_opt величины m, доставляющей минимальное значение сумме квадратов отклонений) описанием способа измерения экспериментального массива {y_n}

y_n = g(G(x_n) + e_n)

4.4. Особенности вычислительной технологии

Вычислительные трудности при реализации алгоритмов обработки измерительной информации пассивного эксперимента связаны с процедурой обращения матрицы X^TX системы нормальных уравнений

(X^TX)^-1b = X^Ty         (3.16)

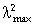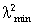Как показывают результаты вычислений, обусловленность информационной матрицы X^TX существенно хуже, чем матрицы X. Если l_max и l_min - наибольшее и наименьшее сингулярные числа матрицы X, а и - матрицы X^TX, то при небольшом l_N число 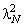 может иметь порядок, сравнимый с порядком погрешностей. В результате матрица X^TX становится почти вырожденной, тогда как матрица X таким свойством не обладает.

При решении плохообусловленных задач МНК используют методы псевдообращения, обеспечивающие работу вычислительных процедур в условиях вырожденности. Псевдообратная матрица X^* существует для любой матрицы X, и для любого вектора

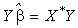
является вектором с минимальной нормой среди всех векторов, минимизирующих сумму квадратов отклонений .

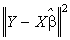Сравнительный анализ экспериментальных данных с помощью различных подходов обращения матриц позволяет выделить прямой метод Гревилла, позволяющий работать непосредственно с матрицей X. Эта матрица лучше обусловлена, чем матрица X^TX. В результате существенно повышается устойчивость к погрешностям округления.

В случае использования нелинейных по параметрам моделей возникает проблема оценок коэффициентов регрессии. При некомпактности априорного множества параметров такая оценка может вообще не существовать (не достигается минимум суммы квадратов отклонений).

Алгоритмы минимизации суммы квадратов, основанные на методе Ньютона-Гаусса, сводятся к линейной аппроксимации функции регрессии