Введение
Моделирование является мощным методом изучения природных явлений или технических процессов. Фактическая цель исследований заключается в построении такой системы параметров, которые необходимым и достаточным образом определяют динамику натурных процессов при изменении начальных условий. Различие, между аналитическими и экспериментальными методами заключается, прежде всего, в том, что при использовании первых рассматривается, как правило, идеализированная модель явления, а при вторых изучаются либо аналоги, либо собственно натурный процесс, развивающийся в реальной среде.
Установление автомодельного характера процесса значительно упрощает анализ результатов исследования. Однако подобное развитие событий является крайне редким успехом. Чаще всего исследование сводится к анализу большого количества и почти всегда разнородной информации. В этих условиях особое место в процессе исследований занимает визуализация полученных результатов (построение графиков функций, эпюр параметров, изолиний скалярных величин или векторных полей и т.д., и т.п.) и непосредственно связанная с ней проблема интерпретации.
В качестве иллюстрации на рисунке (a) приводится визуализация промежуточных результатов вычислительного эксперимента, в котором была допущена незначительная логическая ошибка. В результате была потеряна монотонность решения, первоначально по одному параметру в локальной достаточно ограниченной части расчетной области, которая впоследствии существенно расширилась. При этом контроль вычислений по интегральным параметрам задачи оставался стабильным во все время расчета и не позволял сделать заключения о возможной ошибке. Оперативно проведенная процедура визуализации позволила - во-первых, установить факт наличие ошибки, а во-вторых, примерно определить характер и происхождение последней. Результаты вычислительного эксперимента проведенного после устранения ошибки приводятся на рисунке (в).
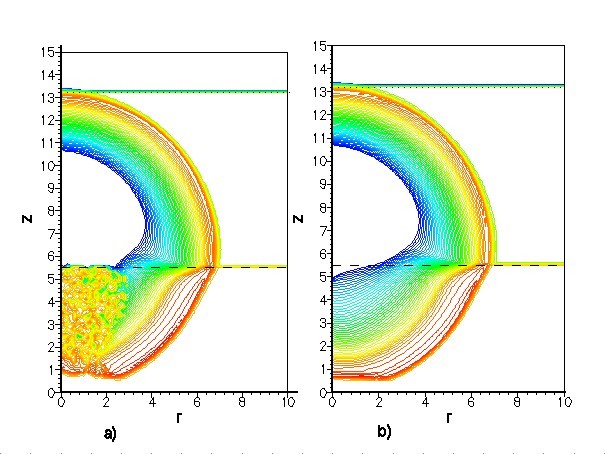
В настоящем курсе лекций рассматривается процедура визуализации результатов вычислительного эксперимента при помощи двух графических приложений:
1) GNUplot'а - командного процессора интерактивной машинной графики, принципы работы которого и излагаются в основном; а также
2) TECplot'а - проблемно-ориентированного графического приложения, при помощи которого, в качестве примеров, осуществляется визуализация и элементарный анализ результатов вычислительных экспериментов по моделированию нескольких газо и гидродинамических задач.
С учетом этих обстоятельств во введении, в дальнейшем, коротко описываются назначение и основные элемент синтаксиса графического приложения GNUplot.
GNUplot - управляемая из командой строки диалоговая программа предназначенная, для построения функций, заданных аналитическим или табличным образом, в виде файлов-данных.
При этом GNUplot различает команды и имена функций, написанные строчными или прописными буквами. Для обозначения любых директив могут применяться соответствующие аббревиатуры, при условии, что смысл принятого сокращения понимается однозначным образом. В командной строке может указываться любое число команд, которые отделяются друг от друга точками с запятой. Исключение составляют команды <load> и <call>, которые должны быть заключительными командами в списке. По команде <load> файлы загружаются в указанном порядке. Когда никакие файлы не загружаются, GNUplot переходит в диалоговый режим. Специальное имя файла "-" используется, чтобы обозначить стандартное обращение к программе. Некоторые строки команд заключаются в кавычки, которые могут быть или ординарными или двойными.
В командной строке gnuplot'а управляющие директивы должны появляться в надлежащем порядке, хотя нежелательные, как правило, просто игнорируются. Например, если полная команда (в условной форме) имеет вид - " команда a b c ", то " команда a c " весьма вероятно будет работать, но попытка ввода команды - " команда c a", скорее всего, приведет к сообщению об ошибке. Командная строка может продлеваться, т.е. включать несколько последовательных команд ввода, каждая из которых отделяется друг от друга косой чертой (\). При этом наклонная черта должна быть последним, характерным знаком на каждой линии командной строки.
В командных директивах фигурными скобками {} обозначаются необязательные аргументы, а вертикальной чертой | отделяются взаимно исключаемые варианты. Угловые скобки < > используются, для обозначения изменяемых параметров.
Общее правило синтаксиса и пунктуации в интерактивном графическом пакете - GNUplot, заключается в том, что ключевые слова и опции следуют в определенном порядке. Опции и любые параметры окружения отделяются друг от друга пробелами. Списки и координаты разделяются запятыми. Минимальное и максимальное значение переменной величины - диапазон, заключаются в квадратные скобки [] и разделяются двоеточием. Текст и имена файлов заключаются в кавычки " ". В некоторых случаях используются круглые скобки ( ). Фигурные скобки {} применяются также и, в том числе, для специальных целей.
Запятые используются, при разделении координат в управляющих командах: set arrow, set key, set label; аргументов в командах set dgrid3d, set dummy, set isosamples, set offsets, set origin, set samples, set size, set time и set view; в списках меток на осях координат и в т.п. случаях.
Команды, которые вводятся на одной командной строке, разделяются точками с запятой ; .
В круглые скобки заключаются наборы явных меток на осях координат (в противоположность циклической разметке осей). В командах - fit, plot, replot и splot круглые скобки применяются в целях указания на вычисления в фильтре {using}. Круглые скобки и запятые также используются, как обычно, в примечании к описанию функции.
Квадратные скобки [] используются, чтобы разграничить минимальные и максимальные диапазоны значений переменных в командах set, plot и splot.
Фигурные скобки применяются также для обозначения комплексных чисел. Например: обозначение {1,2} соответствует комплексному числу - 1 + 2i.
Более подробно правила синтаксиса и пунктуации рассматриваются при обсуждении конкретных команд, используемых при визуализации результатов вычислительных экспериментов на базе интерактивного графического пакета - GNUplot.